Asymmetric Key Cryptography
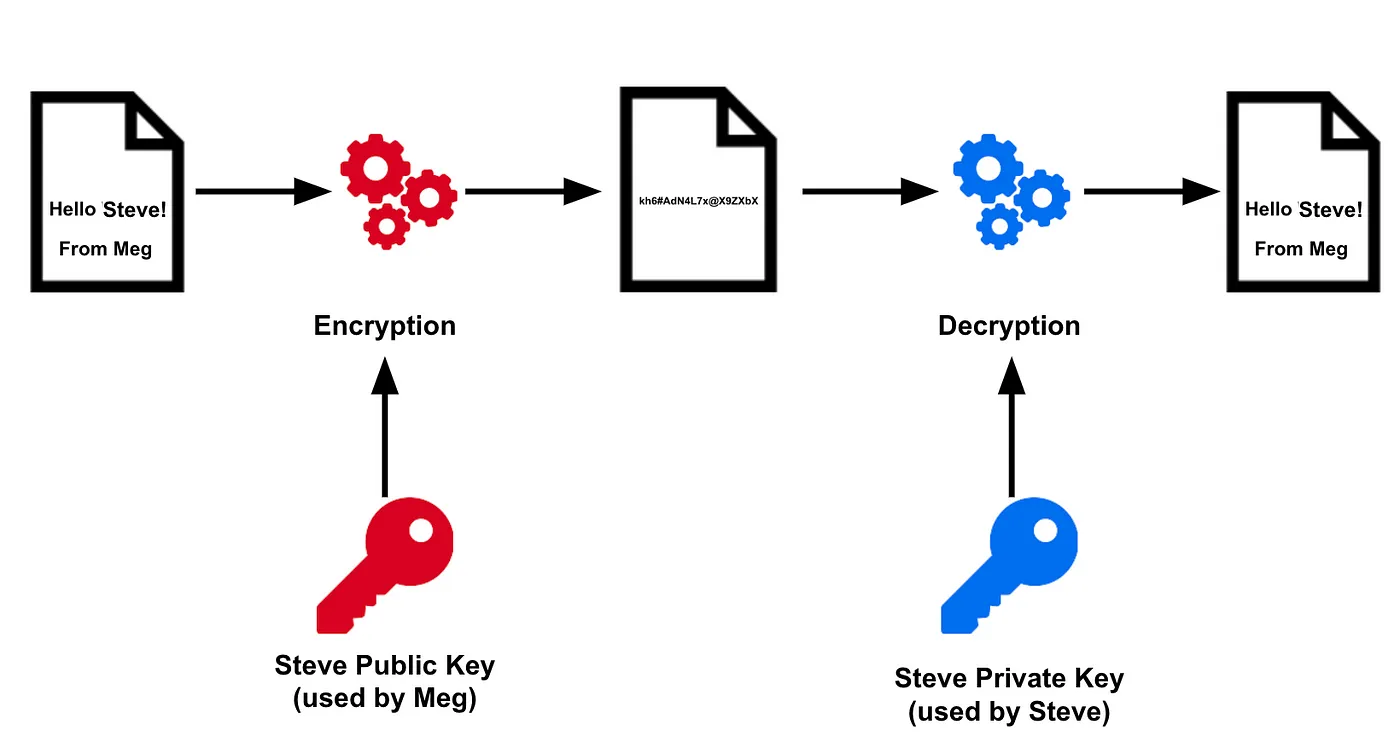
Asymmetric key cryptography (aka public key cryptography) is the concept of using a public and private key to encrypt and decrypt data. The public and private keys are linked mathematically. In asymmetric cryptography both Steve and Meg will use their own unique private keys to encrypt a message.
In the example below Meg uses Steve’s public key to encrypt a message for Steve’s eyes only. Once Steve receives the message he can decrypt by using his private key. If a bad actor was somehow able to intercept our message they would be unable to decrypt it (unless they had Steve’s private key … which they shouldn’t since it’s PRIVATE!)
Strengths of Asymmetric Key Cryptography
- Asymmetric cryptography is scalable. Each additional user require only one new public-private key pair.
- Asymmetric cryptosystems allow for key revocation mechanisms. This provides us with easy and effective user removal.
- If a users private key is compromised only that user must regenerate a key pair. It does not affect anyone else using the cryptosystem
- Asymmetric key encryption can provide integrity, authentication, and non-repudiation.
- We can freely share our public key (our private key can not be derived from our public key); Therefore, we do not need a preexisting, secure communication channel.
Weaknesses of Asymmetric Key Cryptography
- Asymmetric key encryption is much slower than symmetric key encryption
Asymmetric Key Ciphers
RSA
RSA is the most popular and widely used public key cryptosystem.
The strength of RSA is dependent on the difficulty of prime number factorization.
RSA keys can vary in length (the larger the key , the harder it is to crack)
ElGamal
ElGamal expands the Diffie-Hellman algorithm to an entire public key cryptosystem. This algorithm uses difficulty in discrete logarithms to ensure security.
Elliptic Curve
Elliptic Curve Cryptography (ECC) is based on the difficulty in elliptic curve discrete logarithms.
ECC is much more difficult than both the standard discrete logarithms (El Gamal and Diffie-Hellman) and prime number factorization (RSA). A 1,024-bit RSA key is equivalent to a 160-bit ECC key.
Hashing
A hashing function is a one-way function. If we take some text (of an arbitrary length) and we ‘hash’ it using one of multiple hashing functions covered below, we cannot use the hash created (fixed length) to go back to the original text.
Hashing is deterministic. The same text will always produce the same hash output.
Why would we want to use hashing? Integrity. As long as we have the hash of the original file, message, etc. We can hash the file, message we receive and compare the hashes.This provides us with indefinite proof that the original has not been modified.
Hash Functions
###Message Digest (MD) There are 3 versions of Message Digest:
MD2 — Pads the original message until the length is a multiple of 16 bytes and appends the 16-byte checksum to the end of the message.This generates a 128-bit message digest. This hash function has been proven to have collisions and should no longer be used.
MD4 — As processing power advanced , MD needed to increase its level of security. MD4 pads a message to until it is 64 -bits smaller than a multiple of 512 bits. Three rounds of computation are performed on the 512-bit block resulting in a 128-bit message digest. This hash function is no longer suitable and should not be used.
MD5 — Similar to MD4, MD5 processes 512-bit blocks using the same padding (64-bits smaller) and produces the same size message digest (128-bits). MD% differs in that it uses 4 distinct rounds of computation. MD5 is no longer suitable and should not be used
Secure Hash Algorithm (SHA)
There are 3 versions of Secure Hash Algorthim:
SHA-1 — Takes input of any length, processes the message in 512-bit blocks (pads until message length is a multiple of 512), and produces a 160-bit message digest. SHA-1 has weaknesses.
SHA-2 — There are 4 variants of SHA-2, SHA-2 is generally considered secure
- SHA-256 … produces a 256-bit message digest, uses 512-bit block size
- SHA-224… produces a 224-bit message digest, uses a 512-bit block size
- SHA-512… produces a 512-bit message digest, uses a 1,024-bit block size
- SHA-384…produces a 384-bit message digest, uses a 1,024-bit block size
SHA-3 — Theoretically SHA-2 suffers from the same weakness as SHA-1. SHA-3 is a replacement for SHA-2